3 The Role of Prediction in Science
Supervised machine learning is the discipline of producing high-performing prediction models. While the complex dance between prediction and science is age-old, supervised machine learning is relatively young. Let’s find out how this algorithmic approach to learning from data fits into science.
A prediction is an educated guess about an unknown outcome based on current information, such as predicting tomorrow’s weather or the 3D structure of a protein from its amino acid sequences.
Rattle and a group of machine learning advocates presented a petition to the Elder Council of Raven Science. It contained a series of prediction problems, all of which could be solved by machine learning, such as predicting tornadoes or distinguishing poisonous berries from healthy ones. The Council began a difficult philosophical debate: What role should prediction play in Raven Science?

3.1 Scientific theories produce predictions
Since this book has “science” in the title, we are obliged to mention Einstein and his theory of general relativity, one of the biggest success stories of science. Inspired by theoretical and philosophical reflections such as the principle of relativity, Mach’s principle, and the equivalence principle1, Einstein described a theory according to which gravity is a geometric property of space and time. When Einstein developed his theory between 1907 and 1915, it was, unlike his theory of special relativity, not based on novel empirical observations that the old theory did not account for. Instead, Einstein was driven by intuition, a desire to generalize, and mathematical beauty. Still, Einstein’s theory provided what elevated it beyond purely philosophical speculation: It made predictions.
Einstein’s theory of general relativity predicted that:
- Black holes exist.
- Time slows down near massive objects.
- Gravity bends light, makes waves, and affects the red shift in light.
- Massive rotating objects can drag space-time with them, also called the Lense-Thirring precession.
All of these predictions have been confirmed empirically. Some predictions were confirmed soon after Einstein formulated his theory, such as that gravity bends light, which was observed by Eddington and Dyson in 1919 at a solar eclipse. Others, like the existence of gravitational waves, took until 2015 to be confirmed because they required complex new technologies of measurement. It is surprising how long Einstein’s theory has lasted and how correct its predictions are until today – the general theory of relativity is among the best-tested theories in science.
Scientific theories are abstract and universal explanations for phenomena that have strong and diverse evidential support.2 They are strongly tested and cohere with other theories. Theories are thus widely accepted in their fields. Furthermore, theories are not necessarily quantitative. Some of the most important scientific theories are qualitative, such as the germ theory of disease, Darwin’s theory of evolution, and cell theory.
3.2 Prediction can be the goal of science
Less well-known than Einstein’s story is the story of Lewis Fry Richardson, the first person to predict the weather using numerical methods. Besides meteorology, Richardson was an interesting and widely skilled character: he developed a sonar after the tragedy of the Titanic, he found inconsistencies in the measurement of the length of coasts that later inspired Mandelbrot for his theory of fractals, and he was a convinced pacifist and brought quantitative methods to study peace and conflicts between nations.
When Richardson started to work on meteorology, weather forecasting was largely based on experience with similar weather conditions. He wasn’t the first to propose the use of physical theories in weather forecasting, but he was the first to test his numerical model in practice. He developed a mathematical model aimed at predicting the weather:
- He divided a weather map into squares of 200km side length.
- He subdivided each of the squares into layers according to their respective heights.
- He listed all the physical equations he deemed important to model the dynamics.
- He solved the respective nonlinear partial differential equation to predict air pressure, wind speed, and temperature for two of the squares.
Scientific models are typically mathematical representations of aspects of phenomena that allow scientists to predict, explain, or reason about these phenomena. Models can be grounded in theory or even be applications of theories to a specific context. For instance, Richardson used theories from physics to build his weather forecasting model. However, models don’t have to be closely tied to theory. They can also rely on data or common sense. Contrary to theories, models are often more concrete with a smaller scope and more practical. Evidence incompatible with the model just limits the scope of the model, but an otherwise useful model might still survive. Different models for similar aspects of reality can coexist in a field even if they are in conflict.
Unfortunately, his first attempts were unsuccessful. It took him six weeks to make a weather forecast for a six-hour time frame. Even worse, his predictions were pretty far off! Nevertheless, methodologically, he was on the right track; while first ignored after its publication in 1922, his book “Weather Prediction by Numerical Process” is now a modern classic in meteorology. Up until today, scientists use numerical methods, physical measurements, and physical theories to forecast the weather [2]. Fortunately, numerical weather forecasts have substantially improved since Richardson’s first attempt. The availability of atmospheric data, e.g., via airplanes or weather stations, and even more importantly, the access to electronic computers that can solve differential equations efficiently in real-time, allow to predict the weather (at least within 24 hours) reliably. Weather forecasts have become so reliable that when you ask a friend about the weather at the moment, she may check her weather app instead of looking outside …
3.3 Prediction and science are inseparable
Prediction was central to both Einstein’s general theory of relativity and Richardson’s weather forecasting. If the predictions of general relativity had been incorrect, the theory would have been thrown on the scrap heap of science, no matter how beautiful it was. Similarly, if numerical weather forecasting did not work, it would be ignored; in fact, this is exactly what initially happened to Richardson when he proposed his theory.
Predictions played different roles in both cases: In Einstein’s case, the predictions guided new experiments such as the search for black holes, confirmed the theory, and had in the beginning very few practical implications.3 In weather science, on the other hand, accurate prediction is ultimately the goal; also because controlling the weather is at least so far out of reach. Weather predictions are useful: They help people decide when to leave the house, when to harvest plants, how to schedule flights, when to expect catastrophic weather events, and tell your trusted ice shop when to open. Prediction is not a nice byproduct of weather science – it is the goal.
It is widely agreed that prediction is one of the core aims of science [3]. Prediction connects scientific models and theories with events in the world. Science without successful predictions would look a lot like Greek mythology. Pointing out that Zeus is very angry may sound like a nice explanation for the tornado in your yard but how to find out if it is true without predictions? More importantly, will your insurance cover angry gods or only angry birds…
Scientific predictions are statements about data, past events, or the future based on experience or knowledge4. This means that prediction is not just about forecasting the future like tomorrow’s weather. Predictions can also concern the past. The astronomer Johannes Kepler predicted for instance in 1614 that the Star of Bethlehem was a planetary conjunction appearing in the year 7 BC. The term “prediction” also covers cases in which you already know the correct prediction. For example, if a medical diagnosis tool correctly predicts past cases, it is coherent with the observed data. Nevertheless, the gold standard for validating scientific models and theories is accurate predictions of unknown (future) events or unseen data.
3.4 Prediction serves many purposes
Taking a birds-eye view of science, you find that predictions are everywhere and serve many purposes [4]:
- Falsifying and confirming hypotheses: Predictions enable falsification. Predictions that are incompatible with experimental data allow you to reject hypotheses, or weaken scientific theories or scientific models. Conversely, predictions that are compatible with experimental data and future observations boost the confirmation of theories and models.
- Providing a standard for comparison: The predictive accuracy of models provides a standard for comparing scientific models that are grounded in reality and independent of how the models work.
- Checking predictability: If you can consistently predict a phenomenon based on a set of information, it means that this set contains the relevant information to determine the state of the phenomenon. However, if you cannot, it may be because the available information is insufficient. Knowing what can and cannot be inferred from certain information is immensely important in science [5].
- Guiding experiments: Predictions can tell you which aspect of a phenomenon to focus on and run experiments on. If models or theories make interesting or extraordinary predictions for borderline cases, you can check them by running experiments.
- Enabling practical applications of science: Science must always be seen as embedded in a larger economic and social process. Predictions can be used for planning, making processes more efficient, and automating them. Predictions are a way in which science pays off societal investments.
Scientific hypotheses are statements about the world that can be tested experimentally and be falsified. These statements can concern predictions or explanations of phenomena. General hypotheses that have been rigorously tested can become scientific theories. The origin of disease in viruses was a hypothesis before it turned into a theory after it had been rigorously tested. In some contexts, entire models are referred to as hypotheses, meaning that the model is the true or best description of the phenomenon within a given class of models.
3.5 Scientific models may interpolate and extrapolate
Weather forecasting and Einstein’s relativity theory are great examples of two different modes of prediction:
- Interpolation describes the prediction of known data that has been part of the model construction or data highly similar to it.5 Given a reasonable notion of similarity, interpolating works by a simple principle – treat similar data similarly. Data for which you know the true state forms the basis for predicting similar data for which you don’t. For instance, in weather forecasting, you might have a track record of past cloud formations and their corresponding amount of precipitation. Interpolation means to predict the precipitation of new clouds solely based on the precipitation of similar past cloud formations.
- Extrapolation is complementary to interpolation. It concerns predicting data for which you have no similar data available. Extrapolation requires more than just treating similar data similarly. For extrapolation, domain-specific background knowledge must be leveraged. The prediction that very heavy stars may collapse into black holes was one consequence of Einstein’s theory of relativity and was first drawn by Karl Schwarzschild. “Observations” of black holes didn’t exist when Einstein developed his theory. Instead, the prediction was entirely driven by theory, not by reference to similar events in the past.
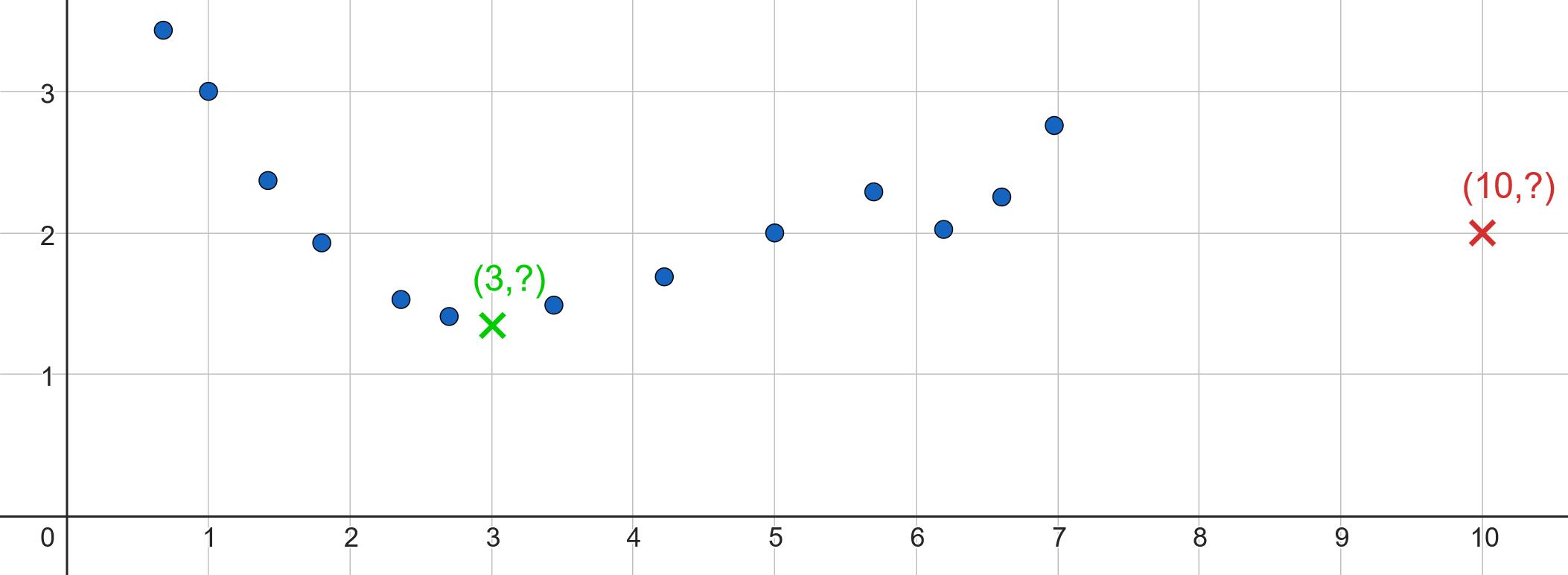
Interpolation and extrapolation play central yet different roles in scientific prediction. Successful interpolation is often taken for granted, as it expresses that the model is consistent with the given data. Extrapolation, or as Popper [7] calls it ‘bold hypotheses’, on the other hand, takes a more prominent role:
- Successful extrapolation can boost your confidence in the background knowledge that informed the inductive bias you equipped your model with.
- It can spark the belief that the prediction model captured relevant aspects of reality [8].
- Also, extrapolation can guide the experimenting process to try to falsify surprising predictions.
3.6 Machine learning is the ultimate interpolation tool
Supervised machine learning’s main strength is the interpolation type of prediction. Supervised machine learning is strongly data-driven rather than relying on background knowledge to predict unknown cases. Extrapolation is therefore not considered a strength of complex machine learning models such as deep neural networks [9], [10], [11]. Some see the current rise of adversarial examples6 as a direct consequence of such failures of extrapolation [12]. But things are not as simple, for these three reasons:
- In machine learning, it is possible to use background knowledge to improve extrapolation, as we discuss in Chapter 8.
- Interpolation and extrapolation can’t be separated as cleanly as Figure 3.1 seems to suggest. The separation depends on the similarity of available and new data, and there is no magic cut-off value where a prediction switches from interpolation to extrapolation. A common formal definition of interpolation is the convex hull of the data, however, this would deem almost every prediction in high-dimensional spaces an extrapolation [13]. Given this definition, interpolation would be a useless notion outside of low-dimensional and linear prediction problems.
- With the right notion of similarity in place, every extrapolation can be phrased as an interpolation. Learning a reasonable notion of similarity might be the primary goal of machine learning.
The principle of relativity says that physical laws are the same for all observers. Mach’s principle states that objects move relative to each other, not in absolute space. The equivalence principle states that gravitational mass and inertial mass are equal.↩︎
In philosophy, as always, there are huge fights about what the terms theory, models, and hypothesis mean. As this is no encyclopedia article on the topic (check out [1]), we won’t do justice to the intricacies of these debates.↩︎
Today, general relativity has strong practical implications as it resulted in making GPS accurate and nuclear energy attainable.↩︎
We constrained our definition of scientific prediction to statements based on experience or background knowledge to take an empiricist perspective. Predictions that are based on neither experience nor knowledge belong to the realm of fortune-telling. Comparing different fortune tellers by their predictions, on the other hand, is again a scientific question.↩︎
In classical math textbooks, interpolation usually only describes the prediction of known data. We will use interpolation in the looser sense to denote predictions for highly similar data as it is often used in statistics or social science research.↩︎
Adversarial examples are slightly modified input data that are predicted incorrectly by the machine learning model.↩︎